ZLATÝ REZ, FIBONACIHO RADA - zdroj Archiweb
Pojem tzv. „zlatý rez" predstavuje proporcní
vztah založený na pomeru dvou jakýchkoliv cástí celku. Jedná se o proporci
cástí A a B takových, že menší cást A se má k vetší B práve tak, jako
se má vetší cást B k souhrnnému celku A a B. Zlatý rez je další proporcní
vztah, který si nárokuje statut všeobecného harmonického zákona s polem
pusobnosti zahrnujícím výtvarné umení, hudbu, architekturu, ale i biologii
ci plastickou chirurgii.
Údajne tento pomer použili již starí Egyptané
pred témer peti tisíci lety pri stavbe pyramid. První písemné zmínky o zlatém
rezu pocházejí z antiky, z helénistického Recka od Eukleida (kol.
340-287 pr. n. l.). Krome Eukleida se v antice zlatým rezem zabýval i umelec
Feidias (sochar, malír, zlatník a architekt), a to již v 5. století pr.
n. l. Postavil známý athénský Parthenon na Akropoli, jehož základem je zlatý
obdélník (viz dále) a zlatý pomer nalezneme i na prucelí této stavby
. Po Feidiovi bylo podle nekterých pramenu ve 20. století zavedeno oznacení
pro zlaté císlo (fí). Jiné zdroje uvádejí, že toto oznacení je na pocest nikoli
Feidia, ale Leonarda Pisánského (asi 1170-1240) zvaného Fibonacci. Jméno tohoto
významného matematika souvisí se zlatým císlem spíše po matematické stránce
(viz dále). Teoretik Vitruvius, autor 10-ti knih o architekture, se zabýval
císelnými závislostmi a proporcními vztahy. Tvrdil, že bez techto znalostí
není možné postavit krásnou budovu. Podle Vitruvia je estetika budovy založena
na císelných vztazích odvozených z proporcí lidského tela. Dnes již víme,
že pomery velikostí cástí lidského tela se casto blíží opet zlatému císlu.
V moderní architekture užíval zlatý rez Le
Corbusier (1887-1965). Zabýval se geometrií, pres niž se snažil pochopit
fungování vesmíru a organické prírody. Príroda žije v harmonii. Clovek
jako jedinec vyšel z prírody, prírodní zákony utvárejí jeho život. Musíme
poznat nejdríve tyto zákony a žít v souladu s nimi, jenom tak si
zajistíme pocit harmonie. Zároven tvrdil, žeje príroda substancí matematiky,
která se na první pohled jeví jako hra propletených událostí. Proto, aby si
clovek zajistil odpovídající prostredí promítl systém prírody do geometrie.
Pomocí geometrie hledal dokonalou proporci, kterou pro nej predstavoval práve
zlatý rez. S jeho pomocí se snažil vymyslet univerzální proporcní jednotku,
která by vycházela z lidské postavy, a která by pak pri použití nejlépe
vyjadrovala vlastní cíl, tedy sloužit díky úcelnosti práve cloveku....byl
to MODULOR.
"Matematika
je velkolepá struktura vytvorená clovekem proto, aby mu poskytla pochopení
vesmíru"
LE CORBUSIER
LE CORBUSIER
Zlatý rez vyjádrený matematickým vzorcem: „ A : B = B : (A+B) "
Zlatý rez vyjádrený geometricky:
 |
POZN: geometrických konstrukcí zlatého rezu
je nekolik, zobrazená varianta je nejcastejší
Zlatý rez lze krome prostredku geometrie vyjádrit
i jako pomer jedné k iracionálnímu císlu phi
(cti „fí"), vyjádrenému pomocí vzorce (v5-1)/2), s hodnotou tedy
približne 0,61803 (tzv. zlaté císlo).
Existuje také císlo Phi s velkým P
na zacátku a toto se liší od phi práve o jednu celou. Phi je tedy približne
1,61803 a vyjadruje se vzorcem (v5+1)/2).
Phi je duležité predevším proto, že udává hladinu, k níž se postupne
více a více približují hodnoty takzvané Fibonacciho rady.
Existuje ješte další možnost, jak se dopracovat
ke zlatému císlu, a to bez použití geometrie, delení úsecky. Se zlatým císlem
úzce souvisí posloupnost prirozených císel (tzv. Fibonacciova
posloupnost), kterou sestavil Ital Leonardo Pisánský zvaný též Fibonacci
(žil na prelomu 12. a 13. století v Pise). V roce 1202 vydal latinsky
psané dílo „Kniha o abaku" („Incipit Liber Abbaci Compositus a Leonardo
filius Bonacci Pisano"). V této knize shrnul všechny tehdejší znalosti
o aritmetice a algebre. Šlo o jednu z prvních knih v Evrope,
která ucila používat desítkovou soustavu. Do té doby se používaly pouze rímské
císlice. Fibonacciho rada je rada celých císel, kde následující clen je vždy
souctem dvou predcházejících clenu. Prvním clenem v rade je císlo 1,
druhým opet 1, protože pred císlem 1 nalezneme pouze 0. Dále rada pokracuje
císlem 2 coby souctem 1+1. Pocátek rady proto vypadá následovne: 1,1,
2, 3, 5, 8,13, 21, 34, 55, 89,144, 233, 377... Pomer jednotlivých následujících
císel této rady se približuje pomeru zlatého rezu a tedy i císlu Phi.
Jmenovite 1/1=1, 2/1=2, 3/2=1,5, 5/3=1,666..., 8/5=1,6,13/8=1,625, 21/13=1,61538...,
a bylo by možné pokracovat s výsledky stále bližšími k císlu Phi.
Fibonacciova posloupnost je nejcasteji zadávána
pomocí tzv. rekurentního vzorce, to znamená, že není dán vzorec pro prímý
výpocet libovolného clenu posloupnosti, ale vztah pro výpocet nekterého clenu
posloupnosti pomocí nekolika clenu predcházejících. Obecný rekurentní vzorec
vypadá následovne:
Pn+k = d
-pn+k-1 + c2-pn+k-2 +... + ck-pn ,
kde pi
jsou cleny posloupnosti, c1,.., ck
(jsou konstanty a n, kjsou prirozená císla. Tímto predpisem jsme vyjádrili
(n+k)-tý clen posloupnosti pomocí
k predchozích clenu. Císlo k
se nazývá rád rekurentního vzorce.
Fibonacciho princip funguje v prírode
aniž bychom o nem meli ponetí. Sám autor ho vyzkoušel pri pokusu o rozmnožování
králíku za ideálních podmínek. Uvedený príklad se muže zdát jako odtržený
od reality, ale dalším dukazem muže být rozmnožování vcel. Fibonacciho císla
mužeme nalézt také v poctech okvetních kvítku, kupríkladu: 3 (lilie,
kosatec), 5 (pryskyricník, karafiát), 8 (stracka), 13 (blatouch). Ješte zásadnejší
se však zdá být struktura rozmístení semen v semenících kvetin ( slunecnice...),
semen šišek, kaktusu, usporádání listu nekterých kvetin nebo schránek morských
korýšu (viz.obr.)
 |
Fibonacciho rada se zde ukazuje být vzorcem
pro optimální usporádání. Zlaté císlo lze tedy skutecne zavést nejen jako
pomer délek dvou cástí úsecky, ale i jako limitu výše zmínené Fibonacciho
posloupnosti.
Znalost hodnoty zlatého císla není k bežnému
životu nezbytná. Nicméne je zajímavé, jak se pomerem zlatého rezu rídí príroda.
Hledání zlatého rezu na rostlinách, schránkách mekkýšu, v krystalických
strukturách látek, ba dokonce i na lidském tele by vydalo na nemalou
knihu. To vysvetluje, proc se tento pomer lidem od pocátku civilizace tak
líbil (a doposud líbí). Prestože o nem vetšina z nás neví, naše
oko je na nej zvyklé. Pomer zlatého rezu vnímáme jako prirozenou vec. Proto
jej i v soucasnosti využívají napríklad architekti, designéri, malíri
nebo fotografové (obcas i neúmyslne) pri své práci.
MODULOR V TEORII
LC byl doslova ucarován zlatým rezem. Tento
proporcní systém používal nejen pri rozvržení fasád domu s horizontálními
okny, ale též v interiéru staveb, napr. pri umistování umeleckých del.
V období druhé svetové války odchází LC z Paríže do Vichy. Poprvé
v roce 1941 zacíná vytváret svuj vlastní proporcní kánon, který nazývá
modulorem (mod/ modus - norma, dor
- zlato). Chce vytvorit ideální proporci architektury, prostoru, která by
byla ve vzájemné harmonii s clovekem. Svuj výsledek vydává knižne v roce
1948 v první knize Le Modulor
(Paris) a v roce 1955 druhý doplnený díl Le
Modulor 2 (Paris).
Podkladem pro výpocty a zároven pro spekulování
predstavuje „typické" lidské telo prumerného Evropana. Mustr lidského tela
je logický, vzájemný vztah cloveka (tela) vuci architekture má historické
koreny už z antiky a pozdeji z renesance. LC si subjektivne definoval
svuj antropologický vzor, sám tvrdil, že jako architekt - umelec má na to
právo. Jak troufalé je, že si jako vzor vybral mužské telo o výšce prumerného
Evropana 175 cm. Tuto výšku pozdeji
upravuje na hodnotu 183 cm nejspíše
proto, že pri delení zlatým rezem vycházejí „hezcí" císla. Skica modulora
nepredstavuje telo „prumerného" Evropa, ale jakoby zobrazovala archaickou
postavu reckého atleta: štíhlý pas, široká ramena a na nich malá hlava. Oznacuje
3 vzdálenosti na lidském tele, jaké tvorí po Fibonaccim radu zlatého rezu.
Mezi nohou, pupíkem, hlavou a prstem zvednuté ruky. Následne delí výšku „prumerného"
Evropana 175cm v pomeru zlatého rezu na merítko 108,2-66,8-41,45-25,4.
(hodnota 175 cm je spíše výškou typického Francouze než Evropana ). Tato poslední
hodnota predstavuje presne 10 palcu, nalézá tímto i spojitost s anglickým
palcem (to ovšem neplatí pro vyšší hodnoty ). Tato císla dostávají lidskou
podobu, rozhodující body pro prostorové usporádání. Jsou tedy antropologická.
Grafické zobrazení prináší odpoved :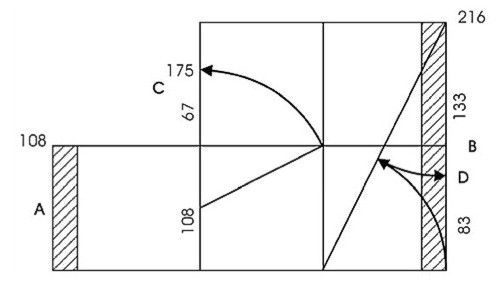 |
dvojnásobná jednotka........................................................................B (= 216)
Zlatý rez - prodloužení.......................................z A = C ( = 175) (108+67)
Zlatý rez - zkrácení...................................................z B = D ( = 83) (143+83)
Od této chvíle lze pripustit, že toto pravidlo
prirazuje hlavním bodum prostoru lidské podoby, a že jimi vyjadruje jednodušší,
podstatnejší, matematický vývoj hodnot. Totéž u jednotky, jejího dvojnásobku
a jejích obou prodloužených nebo zkrácených zlatých rezu. Aby se stal modulor
antropologickou normou, musel být universální pro ruzné délkové jednotky.
Proto ho LC prevádel z cm do stop nebo palcu.
„Modulor
je merítkový nástroj, který vychází s lidské podoby a matematiky."
LECORBUSIER
LECORBUSIER
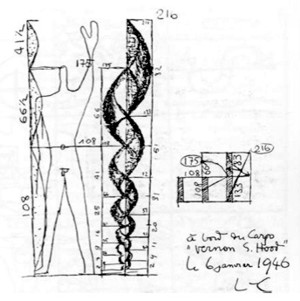 |
První grafické zobrazení Modulora (1946) -
výška cloveka 175cm
V roce 1946 odjíždí LC do USA, kde se setkává
v Princetonu s prof. Albertem Einsteinem, který byl zároven clenem
komise pro volbu místa budovy OSN. Predstavuje mu svuj objev - modulora. Einstein
LC odpovídá: „je to systém, který delá špatné
složitým a dobré jednoduchým".
Po obdržení patentu na modulora, predstavuje
svuj objev verejnosti a vydává knižní podobu Le
Modulor. Troufá si tvrdit, že by mel být modulor na rýsovacím prkne
každého architektka, že se jedná o mimorádnou pomoc v projektování,
která odstranuje veškeré pochybnosti, nesprávnosti.
V roce 1947 vychází Le Corbusierova výška
„prumerného" cloveka naopak opacne ze 6ti anglických stop, presneji z 1828,8
mm. Tou delením dle zlatého rezu získává tzv.cervenou radu smerem od
shora dolu. Když jsou stupne cervené rady pro praktické potreby príliš velké,
vytvárí další tzv. modrou radu vycházející z hodnoty 2260 mm (špicka
prsty zvednuté ruky), taje dvojnásobnou hodnotou cervené rady. Matematickým
delením pomocí zlatého rezu jsou zlomky zaokrouhlovány, tím tak dochází k odlišnostem
7-10 mm nad nebo pod takzvané potrebné hodnoty. Pri prevedení techto základních
hodnot do jiného délkového systému - palcu vzniká další, od toho puvodního
nezávislý systém.
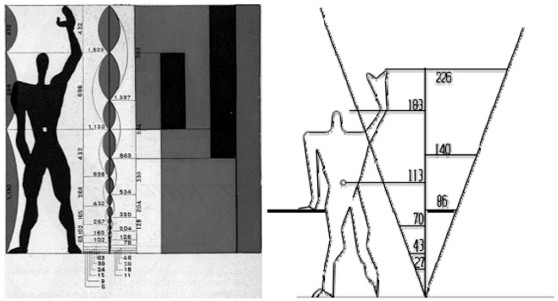 |
Upravené grafické zobrazení Modulora (1947)
- výška cloveka 182,8cm
Pravidlu zlatého rezu náleží 3 hodnoty: 113,
70, 43cm (43+70=113 nebo 113-70=43). Pri scítání: 113+70=183, 113+70+43=226.
Tri poslední hodnoty 113, 183 a 226 cm odpovídají vymezenému prostoru, který
zaujímá clovek o výšce 180 cm. Pri použití pravidla zlatého rezu na hodnotu
113 cm vyplývá 70 cm. Tak vzniká první rada, tzv. cervená, 4-6-10-16-27-43-70-113-183
atd... Pri použití pravidla zlatého rezu na hodnotu 226 cm (2x113) vyplývá
140-86cm. Tak vzniká druhá rada, tzv.modrá, 3-5-8-13-20-33-53-86-140-226-366-592
atd... Nekteré hodnoty z cervené a modré rady mají pozoruhodný vztah
k hodnotám lidského tela.
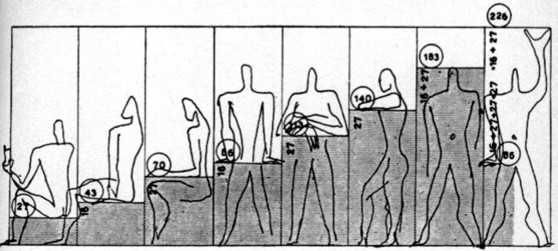 |
Tabulka predstavující prostor,jaký zaujímá
lidské telo v ruzných polohách
Své teoretické objevy prezentuje v roce
1951 na Trienále v Miláne, kde soucastne probíhal kongres o proporcích
za úcasti predních vedcu, matematiku, estetiku, architektu a dalších. Modulor
nezustává pouze v teoretické rovine, LC na jeho základe navrhuje v 50-tých
letech 20.století inovativní stavbu - obytný dum, který svým vnitrním usporádáním
a míšením ruzných funkcí do té doby nemel v architekture obdoby!
MODULOR V PRAXI
> L'Unité d'HabitationG. L. HERSEYLEHO POHLED NA LE CORBUSIERA-MODULORA
Teoretik G.L.Hersley ve své knize s názvem
Architektura a geometrie ve veku baroka venuje
prostor i LC a jeho modulorovi. Geometrie prostupuje celým LC dílem,
ale nikdy nevykrystalizovala v teorii architektury. Autor konstatuje,
že modulor má blízkou spojitost s barokní geometrií R. Fludda, Kirchera
a Keplera. LC se od renesance a baroka distancoval a svým predchudcum vytýkal
racionální symetrii prenesenou do geometrických plánu, on zastával geometrii
asymetrickou. Presto stejne jako oni oslavoval úcinek hudby, lidského tela
jako puvodce merítka, vznešených císel a jejich sérií a sekvencí. Byl prukopníkem
ideální souradnicové síte, kde se nacházely bunky ideálních ctyrúhelníku,
užívaných v renesanci a baroku... To signalizuje odkud vycházel, i když
navenek prezentoval svoji teorii a sám to nepriznává.
Pri delení lidského tela na tri intervaly
(od nohy k pupíku, od pupíku k temeni hlavy a od temene hlavy k prstu
vztycené ruky) získává tri hodnoty: 108, 661/2, 411/2.
Žádná z techto délek ve skutecnosti není Fibonacciho radou a ani neodpovídá
pomeru zlatého rezu! LC tvrdí pravý opak. Pravá Fibonacciho rada vždy zacíná
císlem 1, LC svoji radu zacíná císly 3 a 4, proto mu vycházejí jiné posloupnosti.
( Dukaz: 108 : 661/2= 1,602; 661/2:411/2=
1,624... skutecná hodnota zlatého rezu 1,618).
V první skice modulora se vedle „primitivní" kresby cloveka objevují
další dve merítkové rady vymezující plochy. Možná že mají souvislost s tzv.
sectorem, barokním nástrojem pro merení
ploch a objemu v ruzném merítku. Nekteré hodnoty posloupností jsou podle
Fibonacciho rady, nekteré zase v pomeru zlatého rezu a ostatní jsou zcestné,
mimo tyto teorie. Císlum LC pripisuje intervaly na lidském tele, ale hodnoty
2, 9 a 11 nikdy nemohou pasovat na lidské telo.
Ideál lidské postavy (mužské) jako základního
merítka smeruje do antiky k Vitruviovi. Na neho navazuje Leonardo
da Vinci s kresbou cloveka vepsaného do kruhu a ctverce (1485-1490).
Až doba baroka s sebou prinesla zájem o císla vytvárející lidské
telo. Robert Fludd (1574-1637) skrz
nej chápal podstatu celého kosmu. Za povšimnutí stojí fakt, že i LC renesancní
a barokní predchudci nemeli správné proporce, tak jako práve modulor. Skica
modulora je nedokonalá. Postava má velmi malou hranatou hlavu bez tváre vyznacenou
pouhým obrysem, obdobná je vztycená ruka naopak mohutná bez zobrazených prstu.
LC predchudci hledali duležité proporcní souvislosti i z detailu jako
je lidská tvár, dlan s prsty. LC se o toto vubec nepokusil, že by
bylo grafické ztvárnení duležitejší pred skutecností a nebo kamufluje nedokonalost
jeho postavy?
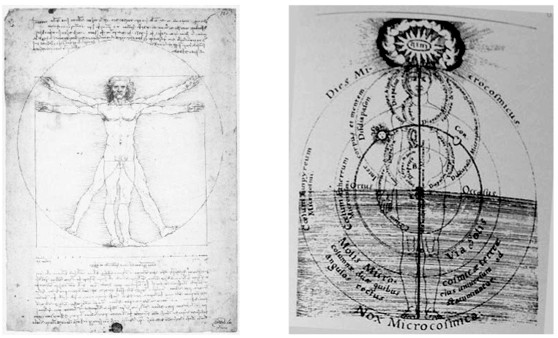 |
Kresba cloveka od L. da Vinciho (1485-90) a
kresba cloveka od R. Fludda (1574-1637)
Presto postava LC má s postavou L. da
Vinciho spolecný duležitý vztah. Obe postavy lze vepsat jak do kruhu, tak
i do ctverce. Stred kruhu tvorí pupík, stred ctverce penis. Naopak u postavy
Roberta Fludda je jejím stredem penis, jako stred všeho. Na finální verzi
modulora spolupracovalo s LC nekolik jeho spolupracovníku vcetne Ellisy
Maillard. Ta puvodní koncept obrací k R. Fluddovi. Pridává kruhy
o ruzných velikostech vycházející ze stredu ctvercu základního nákresu.
Kruhy se vzájemne protínají stejne jako v baroku u Fludda. O vedomém
ovlivnení modulora jeho mikrosvetem není pochyb.
Na záver G.
L. Hersley konstatuje, že modulor nebyl konstruován na základe zlatého
rezu a Fibonacciho rady. Kdyby ano, stacilo by pouze zmenit hodnoty trojdílného
delení tak, aby vycházely správne. Zároven nebylo úcelem LC ho prevádet prímo
do architektury. Tvrzení, že pomer 175:108=1,620 predstavuje hodnotu zlatého
rezu 1,618 je chybné. Pridáním ctvercu,
kruhu do kresby modulora vznikají ciste lineární ctverce, které vytvárejí
moduly. Modulor se tak stal základem modulu...
to bylo výsledkem. Delením ctvercu ve zlatém rezu vznikají další merítkove
rozmanité ctverce, obdélníky, síte, které prevedením do stavitelství mohly
predstavovat pudorysy domu, steny-panely, dvere, okna a takto bychom mohli
pokracovat do jednotlivých detailu objektu.
PRAMENY, LITERATURA:
- http://www.tu-harburg.de/b/kuehn/lec4.html
- http://www.michael-robinett.com/isis/mod-2.htm
- Bakalárská práce „Zlatý rez",Vlasta Chmelíková, Matematicko-fyzikální fakulta, UK v Praze, 2006
- Oeuvre complete Le Corbusier 1946-52
- Le Corbusier, Norbert Huse, Votobia 1995
- Le Corbusier, Rostislav Švácha, Odeon 1989
- Architecture and Geometry in the Age of the Baroque, George L. Herseye, Chicago 2000